Anwendung der Technischen Mechanik auf Tischtennis
Die Links wurden am 30.10.21 verifiziert. Änderung am 30.10.21
Wie beim Fußball, so lässt sich die Kinematik und Dynamik auch beim Tischtennis vorteilhaft einsetzen. Ein gut platzierter Ball braucht kein Zufall zu sein. Sehen Sie sich dazu folgende Videos an:
https://www.youtube.com/watch?v=5tTFCVCfu_o&NR=1
https://www.youtube.com/watch?v=843dyG3Ud7c
Tischtennis WM Finale 2017 Düsseldorf MA Long(CH) vs FAN Zhendong(CH)
Deformation und Festigkeit des Schlägers
Kombination verschiedener Drallrichtungen
Berechnungen zur Kombination verschiedener Drallrichtungen
http://www.noppen-test.de/tischtennis.php
Spielregeln
Richtlinie zur Schlägerkontrolle im DTTB
http://www.noppen-test.de/material.php
Belagliste
http://www.noppen-test.de/spin.php
http://www.noppen-test.de/spiel.php
Seite mit viel Information
http://www.tischtennis.de/fuer_aktive/regeln/
Deutscher Tischtennis Bund
http://www.noppen-test.de/links.php
Links zu weiteren Seiten
http://lange-noppen-tischtennis-tipps.de/
Tipps für Dein Tischtennis Training mit und gegen Materialspiel und Abwehr
https://de.wikipedia.org/wiki/Tischtennisschl%C3%A4ger
Einführung in die Grundlagen, insbesondere von Schläger und Belag
http://www.tischtennis-world.de/schlaeger.php
Zitat: "Der Ball darf nur mit einem Noppengummi (Noppenaußenbelag ohne Schwamm-->höchstens 2mm dick) oder einem Sandwich-Gummi Noppeninnenbelag (höchstens 4mm dick) gespielt werden."
https://de.wikipedia.org/wiki/Reibungskoeffizient
Grundlagen
https://de.wikipedia.org/wiki/Rollreibung
Rollwiderstand
Auf der folgenden Seite werden die für die Bewegung des Balls am Schläger grundlegenden Gleichungen angegeben.
http://itp.tu-graz.ac.at/LV/schnizer/Analytische_Mechanik/node8.html
Die Kräfte und die Bewegungsgleichungen
Erhaltungssätze für Massenpunktsysteme
Gesamtimpuls und Schwerpunkt
Gesamtdrehimpuls
Energiesatz
Das Zweikörperproblem
Elastischer Stoß zweier Massen
Der Stoß auf ein ruhendes Target
Der Stoß zweier glatter Kugeln
Das Zweikörperproblem mit Wechselwirkung
http://wwwex.physik.uni-ulm.de/lehre/krm-2007-2008/node12.html
Einführung in die maßgeblichen Beziehungen. Versuchsbeschreibung
https://de.wikipedia.org/wiki/Stoß_(Physik)
Alles Wissenswerte
Deformation und Festigkeit des Schlägers
Der Stoß des Balls auf den Belag des Schlägers hat eine Reaktion zur Folge, die nicht nur mit der Reibung des Balls auf der Oberfläche, sondern auch mit der Deformation des Belages zu tun hat.
https://www.ballsportbibel.de/tischtennisschlaeger-test/
Verhalten von Schläger und Belag
https://www.tischtennis.net/bester-belag/
https://schoeler-micke.tabletennis-shop.de/Belaege/
Bewegung im konservativen Kraftfeld
Senkrechter Wurf im Gavitationspotential
Wurf in Relativkoordinaten unter Berücksichtigung der Kinetik
Darstellung der Bewegung in verschiedenen Koordinatensystemen
Relativbewegung
Bewegungen unter dem Einfluss von Reibungskräften
https://www.uni-kassel.de/fb10/fileadmin/datas/fb10/physik/oberflaechenphysik/exp2/Lehre/ExpPhysI/Mehrdimensionale-Bewegungen.pdf
Mehrdimensionale Bewegungen
https://de.wikipedia.org/wiki/Wurfparabel
Freier Wurf
https://de.wikibooks.org/wiki/Kinematik
Kinematische Grundgrößen in verschiedenen Koordinatensystemen
http://www.cfd.tu-berlin.de/~bunge/paper/IB199/Struktur/node5.html
Lagrangesche und Eulersche Darstellung
https://www.spektrum.de/lexikon/physik/begleitendes-dreibein/1357
begleitendes Dreibein
http://wwwex.physik.uni-ulm.de/lehre/krm-2008-2009/node13.html
Geschwindigkeit und Beschleunigung im dreidimensionalen Raum
http://itp.tu-graz.ac.at/LV/schnizer/Analytische_Mechanik/node9.html
Bewegte Bezugssysteme. Inertialsysteme, beschleunigte Bezugssysteme
https://de.wikipedia.org/wiki/Beschleunigtes_Bezugssystem
Beschleunigtes Bezugssystem
Die gekrümmte Flugbahn des Balls entsteht durch eine Rotation des Balls. Dabei reißt er Luft mit sich, und zwar in die Richtung, in die er sich dreht (Magnus-Effekt). Benannt ist der Effekt nach seinem Entdecker, dem deutschen Physiker und Chemiker Heinrich Gustav Magnus (1802-1870)
http://www.systemdesign.ch/index.php?title=Fussball#Bananenflanke
Erklärung des Effekts und Formel für die Magnuskraft in vektorieller Schreibweise.
1 Abstoss
2 Abstoss mit Rotation
3 Bananenflanke
Eine hohe Ballgeschwindigkeit ist für einen starken Magnuseffekt wichtig.
Bei manchen Belägen ist die Haftfähigkeit des Balls besonders hoch. Hierdurch lässt sich ein hoher Drall des Balls erzeugen.
Infolge der Rotation wirkt auf den Ball neben der Gewichtskraft und dem Luftwiderstand die Magnuskraft FM. Diese Kraft steht normal zur Geschwindigkeit und normal zur Winkelgeschwindigkeit und kann näherungsweise mit folgender Formel berechnet werden.
FM = π ρ ω r3 v
Dim = kg/m3 * 1/s * m3 * m/s = kg m/ s2 = Masse * Beschleunigung = Kraft N
Anmerkung: Verschiedentlich werden auch andere Werte für die Potenz sowie Beiwerte CM verwendet, was aber leicht zu Problemen hinsichtlich der Dimensionen führen kann.
Aus der Formel für den Weg der Ablenkung s unter einer konstant wirkenden Kraft FM kann ersehen werden, dass der Wert von s quadratisch mit der Zeit zunimmt. Das bedeutet: Die Anwendung des Magnuseffekts ist beim Tischtennis dann angebracht, wenn lange Bälle geschlagen werden. Die überproportionale, nicht lineare Zunahme der Ablenkung ist umso wirkungsvoller, je länger der Flug des Balls dauert.
Kombination verschiedener Drallrichtungen
Manche Spieler glauben, dass ein erfolgreiches Topspinspiel mit einem Schläger erfolgen muss, der folgendes bietet:
· Speed
· Klebevorgang
· Power-Topspin durch Deformation der Belagsoberfläche
Dies kann zutreffen, hat jedoch den Nachteil, dass die Wahrscheinlichkeit, einen Ball zu verschlagen, auch nicht ganz gering ist, weil passend zum Drall des ankommenden Balls ein entsprechender, wohl dosierter Gegendrall erzeugt werden muss. Es gibt jedoch zwei Möglichkeiten, dieses Problem zu vermeiden.
Die erste Möglichkeit beruht auf der Verwendung von langen Noppen. Die biegsamen langen Noppen bewirken eine Schnittumkehr bei der Annahme von Topspinschlägen.
Den Drall des ankommenden Balls einfach weiterzugeben beruht auf der hohen Elastizität und der geringen Reibung der Noppen. Die Energie des Dralls wird durch glatte lange Noppen nicht aufgenommen und bleibt praktisch unverändert. Dadurch behält der zurückfliegende Ball seine Drehung, die aber bei dem Spieler, der ihm den Topspin gegeben hat, die Wirkung hat, als hätte der Gegenspieler den Ball unterschnitten. Die Wahrscheinlichkeit, einen Ball zu verschlagen ist relativ hoch. Dies hat vermutlich zum Verbot bestimmter langer, glatter Noppen geführt. Hier soll darauf nicht weiter eingegangen werden.
Die zweite Möglichkeit besteht darin, einen bestimmten Gegendrall zu erzeugen. Hat der Gegner den Ball unterschnitten, muss man ebenfalls unterschneiden. Die Größenordnung dieses einzuprägenden Dralls muss in der des ankommenden Balls liegen, sofern dieses Prinzip nicht mit einem weiteren kombiniert wird, nämlich dem der Vernichtung der Drallenergie durch Reibung im Zuge einer Querbewegung des Schlägers. Zur Vorbereitung soll zunächst der Kammsche Kreis vorgestellt werden.
https://de.wikipedia.org/wiki/Kammscher_Kreis
Der Kammsche Kreis wird zwar in der Fahrzeugtechnik verwendet, ist aber beim Tischtennisspielen von ebenso hoher Bedeutung. "Die wichtigste Aussage des Kammschen Kreises ist …, dass Längs- und Seitenführungskräfte voneinander abhängen und dass die resultierende Gesamtkraft beider die zur Verfügung stehende max. Haftreibungskraft nicht überschreiten kann." Zielsetzung in der Fahrzeugtechnik ist, dass die Resultierende verschiedener auf den Reifen wirkender Kräfte die Haftreibungskraft nicht überschreiten soll.
Wenn man beim Tischtennis dem Ball einen möglichst hohen Drall geben will, hat man die gleiche Zielsetzung. Es kann sogar vorkommen, dass man den Schläger weniger schnell bewegen muss, um den Haftreibungsbereich zwischen dem Ball und dem Schlägerbelag nicht zu überschreiten und dadurch nicht in den Gleitreibungsbereich zu kommen.
Der andere Fall ist der, möglichst in den Gleitreibungsbereich zu kommen, damit sich der Drall des ankommenden Balls nicht oder kaum auswirken kann. Man kann zwar versuchen durch eine bestimmte Bewegung des Schlägers den Drall des ankommenden Balls zu kompensieren. Dies ist eine häufig angewendete Technik. Wenn man jedoch den Vektor der in der Oberfläche des Belages wirkenden Kraft (die Reaktionskraft infolge Reibung und Deformation des Belages) infolge Stoß und Drall des ankommenden Balls durch eine Kraft infolge Seitwärtsbewegung des Schlägers ausreichend vergrößert, so dass die Resultierende der beiden Kräfte eine Länge hat, die groß genug ist, den Haftreibungsbereich zu verlassen, so tritt Gleitreibung ein. Da der Koeffizient der Gleitreibung wesentlich kleiner ist als der der Haftreibung, verpufft der Schnitt des ankommenden Balls fast wirkungslos, wenn die Deformation und die Gleitreibungszahl des Belages ausreichend klein sind. Der Vorteil daraus ist riesig. Der Gegner kann schneiden wie er will: Es ist praktisch alles wirkungslos.
Die seitliche Bewegung des Schlägers kann so verändert werden, dass sie einen kleinen Winkel mit der Horizontalen einschließt. Dies reicht, um dem Ball einen Drall zu geben, der zwar deutlich kleiner sein kann als mit einem Topspinschläger, für lange Bälle jedoch völlig ausreicht, um den gewünschten Bogen infolge des Magnuseffekts zu erzielen, da bei längeren Bällen die Ablenkung aus der normalen Flugbahn infolge des Magnuseffektes quadratisch mit der Bahnlänge bzw. Flugzeit zunimmt, so dass die Verwendung eines Topspinschlägers in der Regel nicht zwingend ist.
Worauf ist zu achten? Wenn der Ball über- oder unterschnitten ist, muss man den Schläger seitlich bewegen. Die Haftung des Belages am Ball sollte klein sein; um überhaupt einen zu Effekt erzielen, aber nicht zu klein. Weil man auf den Schnitt des ankommenden Balls kaum achten muss, lassen sich die Returnbälle wesentlich sicherer platzieren und die Ballgeschwindigkeit des Returns darf sehr hoch sein. Statt eines Reaktions- oder Defensivspiels kann man öfter zum Angriffsspiel übergehen.
Der seitliche Weg des Schlägers kann einen Winkel mit der Horizontalen einschließen. Wir definieren diesen entgegen dem Urzeigersinn als positiv.
· Bei positivem Winkel erhält der Ball einen Überschnitt. Der Ball sinkt wegen des Magnuseffekts hinter dem Netz schneller. Um diesen Effekt wirksam werden zu lassen, muss man entweder die Reibung des Belags erhöhen (was aber gerade vermieden werden sollte), oder die Flugbahn verlängern. Das heißt, niedrige Bälle sollten möglichst spät, vornehmlich in Tischhöhe oder darunter angenommen werden.
· Bei negativem Winkel erhält der Ball einen Unterschnitt. Er nimmt wegen des Magnuseffekts, der das Absinken infolge Eigengewichts des Balls hindert, eine geradlinige Bahn an. Den negativen Winkel kann man einsetzen, wenn der Ball sich in 2- bis 3-facher Höhe des Netzes befindet. Da er wegen der geradlinigen Flugbahn sehr sicher platziert werden kann, sollte er in Verbindung mit einem High-Speed-Belag regelmäßig zu einem Punktgewinn führen.
Für die Querbewegung des Schlägers steht für den Körper, den Arm und die Hand fast immer unbegrenzt Raum zur Verfügung, weswegen man dem Schläger in Querrichtung die maximal mögliche Geschwindigkeit geben kann. Dadurch kann, obwohl der Belag eine niedrige Gleitreibungszahl hat, dennoch ein ansehnlicher Drall erzeugt werden.
Bei Belägen, bei denen die Vektoren des vorhandenen und des neu erzeugten Dralls addiert werden müssen, ist der resultierende Drallvektor hinsichtlich Größe und Richtung vom Spieler abzuschätzen, was sehr fehleranfällig ist. Die Einschätzung, welchen Drallvektor der abgehende Ball schließlich haben wird, ist dagegen bei dem vorgestellten Konzept sehr gut möglich, da der Drall des ankommenden Balls kaum noch eine Rolle spielt und nicht mehr hinzuaddiert werden muss.
Es ist ohne weiteres möglich, mit einem Schläger, der hohen Speed und geringe Oberflächenhaftung hat, 50 Ballwechsel zu spielen, wobei allerdings taktische Zielsetzungen, wie Punktgewinn, keine Rolle spielen dürfen. Dies zeigt aber, dass bei Verwendung eines High Speed Antitop Schlägers die Taktik und der Speed für einen Punktgewinn die größte Rolle spielen sollten.
Weiterhin soll hinterfragt werden, ob es sinnvoll ist, einen großen Topspin anzustreben. Richtig ist, dass sich bei einem hohen Topspin der Ball am Ende der Flugbahn schneller senkt und dadurch die Wahrscheinlichkeit, dass er über die Platte hinausfliegt, verringert wird. Der Topspin dient wohl in erster Linie der eigenen Sicherheit. Der Winkel aber, den der auf die Platte treffende Ball mit der Platte einschließt, wird größer und somit auch der Winkel, in dem der Ball die Platte verlässt. Er springt daher höher als ein unterschnittener Ball. Das ist für den Returnspieler die beste Voraussetzung, dem Ball im Verlaufe der Querbewegung des Schlägers durch einen leichten Unterschnitt eine geradlinige Flugbahn zu geben, die zudem die kürzeste aller möglichen Bahnen ist. Daher ist der Antitop in Verbindung mit einer Querbewegung und einem dem taktischen Erfordernis angepassten Winkel der Querbewegung zur Horizontalen aus taktischer Sicht optimal.
Berechnungen zur Kombination verschiedener Drallrichtungen
Ein Ball fliegt in horizontaler Richtung auf die senkrechte Fläche des Schlägers zu.
o v0 ist die Schwerpunkt-Geschwindigkeit des Balls vor dem Auftreffen auf den Schläger.
o ω0 ist die zu dem anfliegenden Ball gehörende Winkelgeschwindigkeit.
o N(t) ist die Kraft, die durch den Ball auf den Belag des Schlägers ausgeübt wird. Die Reaktionskraft ist ebenfalls N(t), aber mit der entgegengesetzten Orientierung. Ihr Betrag ist von der Zeit t abhängig.
o N ist der Mittelwert der Kraft N(t) im Intervall Δt.
o t0=0 ist der Zeitwert beim ersten Kontakt des Balls mit dem Schläger.
o t1 ist der Zeitwert, in dem sich die Bewegungsrichtung des Balls umkehrt oder auch, in dem die Geschwindigkeit des Balls in horizontaler Richtung Null ist.
o t2 ist der Zeitwert, in dem der Kontakt des Balls mit dem Belag des Schlägers beendet ist.
o Δt=t0-t2 ist das Kontaktzeitintervall.
o μHaft ist die Haftreibungszahl zwischen Ball und Belag des Schlägers.
o RHaft= μHaft*N ist die Gleitreibungskraft infolge der Normalkraft N.
o μGleit ist die Gleitreibungszahl zwischen Ball und Belag des Schlägers.
o RGleit= μGleit*N ist die Gleitreibungskraft infolge der Normalkraft N.
o RQGleit= μGleit*N ist die Gleitreibungskraft infolge einer Querbewegung. Die Bewegung erfolgt horizontal, oder in einem kleinen Winkel zur Horizontalen. Sie steht senkrecht auf v0.
o Δs ist der Weg des Schwerpunktes S des Balls infolge Deformation des Balls und des Oberflächenbelages.
o w=2* Δs ist der gesamte Weg des Schwerpunktes S im Intervall Δt.
o a ist der Mittelwert der Beschleunigung des S in horizontaler Richtung im Intervall Δt. Er ist eine Konstante. Der Bewegungszustand wird deshalb als gleichmäßige Beschleunigung bezeichnet.
o vz ist die Schwerpunkt-Geschwindigkeit des Balls in Richtung z, das heißt in dem hier gewählten Berechnungsmodell parallel zur Oberfläche des Schlägers.
o Δvz ist die Zunahme der Schwerpunkt-Geschwindigkeit des Balls in Richtung z im Intervall Δt infolge RGleit. Da die Beschleunigung a aus der Formel a=2*w/Δt2 für den Weg bei gleichmäßiger Beschleunigung errechnet wird, sind N=m*a und RGleit= μGleit*N ebenfalls Mittelwerte, so dass vz am Ende des Intervalls Δt ebenfalls aus einer gleichmäßigen Beschleunigung entstanden gedacht werden kann. RGleit ist der Mittelwert der Kraft über das Intervall Δt.
o r ist der Radius des Balls in der Dimension m.
o m ist die Masse des Balls in der Dimension kg.
o I ist das Massenträgheitsmoment des Balls.
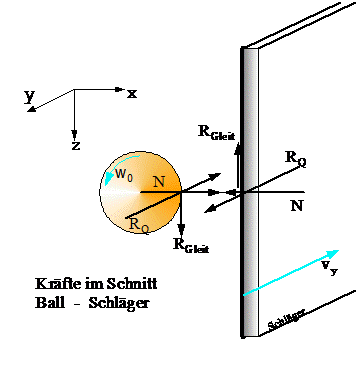
Bild: Kräfte auf den Ball, den Schläger sowie in der Kontaktfläche während des Stoßes.
Während der gesamten Kontaktzeit liegt Gleitreibung vor, weil es eine senkrecht zur Geschwindigkeit des Balls gerichtete Bewegung vy des Schlägers gibt, so dass die Resultierende der Geschwindigkeiten in allen Zeitpunkten des Kontaktzeitintervalls einen Vektor v ergibt, der groß genug ist, die Haftreibung zu überwinden. Eine entsprechende Aussage gilt für die Kräfte.
Falls die Winkelgeschwindigkeit ω0 des anfliegenden Balls klein ist, besteht die Möglichkeit, dass durch Reibungsarbeit die Energie des Dralls aufgezehrt wird, bevor die Ablösung des Balls von der Kontaktfläche erfolgt. Dann wirkt die Kraft RGleit nur über ein Teilintervall von Δt. Die folgenden Berechnungen werden aber unter der Annahme durchgeführt, dass der Drall groß genug ist, um über die gesamte Zeit Δt eine Reibungskraft RGleit zu liefern.
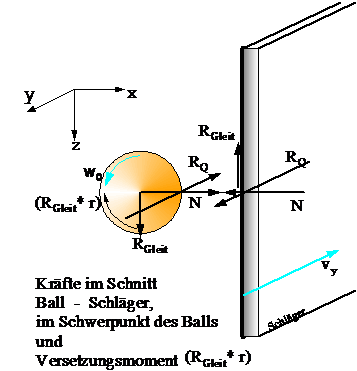
Bild wie vor, jedoch ist die Kraft RGleit, die auf den Ball wirkt, seitlich in den Schwerpunkt des Balls verschoben worden. Daher muss das Versetzungsmoment RGleit* r eingezeichnet werden. Das Versetzungsmoment verringert die Winkelgeschwindigkeit ω0. Die Kraft RGleit im Schwerpunkt S wirkt über das Zeitintervall Δt und bewirkt eine in Richtung z gerichtete Geschwindigkeit vz. Je größer RGleit ist, umso größer ist wegen F*Δt= RGleit*Δt =m*Δvz die Zunahme der Geschwindigkeit vz. Da der Weg zum Netz kurz ist, wirkt sich der Drall auf die Bahn des Balls kaum aus, da die seitliche Ablenkung des Balls infolge des Magnuseffekts mit dem Quadrat der Entfernung zunimmt. Hingegen ist es die Geschwindigkeit vz, die den Ball ins Netz befördern kann, wenn er vom Gegenspieler unterschnitten worden ist.
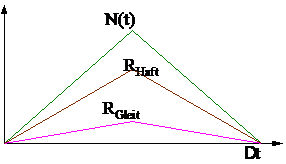
Bild: Stark vereinfachter Verlauf der Kontaktkraft N(t) über das Intervall Δt sowie Verlauf der Reibungskräfte über das Intervall Δt. Für die Berechnung wurde ein konstanter, mittlerer Wert N und RGleit angenommen.
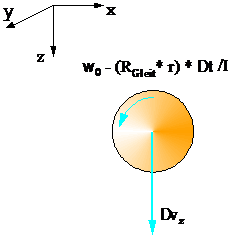
Bild: Bewegung des Balls nach dem Stoß
Die folgende einfache Berechnung soll nicht dazu dienen, die wahren Werte der Geschwindigkeit Δvz zu ermitteln, sondern um zu erfahren, wovon Δvz abhängig ist.
Berechnung dynamischer und kinematischer Größen in Richtung x
Δt ist aus einer Überschlagsrechnung zu ermitteln. Wir nehmen an, dass v0 über den Weg Δs auf 0 abnimmt.
Δt = 2* w/ v0
Beziehung zwischen konstanter Beschleunigung a und Weg w aus der Kinematik
a=2*w/Δt2
Newtonsches Grundgesetz zwischen Kraft N und Masse m für Translationen.
Da a eine Konstante ist, ist auch N eine Konstante, und zwar der Mittelwert der Kraft N(t) im Intervall Δt.
N=m*a
Einsetzung der Beziehung für a
N=m*2*w/Δt2
Berechnung dynamischer und kinematischer Größen in Richtung z
Gesetz für die Gleitreibung
RGleit= μGleit*N
Impuls infolge Gleitreibungskraft
RGleit*Δt=m*Δvz.
Ersetzung der Gleitreibungskraft in Abhängigkeit von N
μGleit*N*Δt=m*Δvz
Auflösung nach Δvz
Δvz= μGleit*N*Δt/m
Einsetzung der Normalkraft in Abhängigkeit von w und Δt in Richtung x
Δvz= μGleit*(m*2*w/Δt2)*(Δt/ m)
Δvz= μGleit*2*w/Δt
Einsetzung der Abschätzung für Δt, ermittelt für die Richtung x
Δvz= μGleit*2*w/(2* w/ v0 )
Δvz= μGleit*v0
Dieses Ergebnis ist recht erstaunlich, weil Δvz nicht von der Dicke des Belages oder der Länge des Kontaktzeitintervalls Δt abhängt.
Das Bestreben muss somit dahin gehen, die Gleitreibungszahl μGleit klein zu halten, damit Δvz einen kleinen Wert annimmt.
Allerdings wird man für den Wettkampf außer einem kleinen μGleit einen hohen „Speed“ haben wollen, so dass die Dicke des Belages und seine Elastizität bzw. das Kontaktzeitintervall Δt dann doch eine Rolle spielen kann. Das beeinflusst aber die erforderlichen Eigenschaften für die Abwehr eines Dralls nicht. Diese Erkenntnis erleichtert die Auswahl des „richtigen“ Schlägers sehr.
http://www.noppen-test.de/spin.php
„Bei hochklassigen Spielern ist Tempo wichtiger als Spin.“ Mit den eben gewonnenen Erkenntnissen kann die Auswahl des richtigen Belages sicherlich besser erfolgen. Ich spiele mit einem Schläger der eine kleine Gleitreibungszahl μGleit, aber hohen Speed hat und finde diese Kombination optimal. Trotzdem ist es kein Problem dem Ball bereits beim Aufschlag einen solchen Drall durch Querbewegung des Schlägers zu geben, dass der Ball beim ungeübten oder unaufmerksamen Gegenspieler im 45-Grad-Winkel aus der Richtung fliegt.
http://www.noppen-test.de/gorilla.php
Die folgenden Zitate sollen belegen, dass es für das vorgestellte Konzept geeignete Schläger gibt. (Unterstreichungen wurden zugefügt)
· „Dr. Neubauer GORILLA ist unsere Antwort auf das Verbot von glatten langen Noppen. Spieler, die bisher mit unseren langen Noppen-Belägen 'Super Block', 'Inferno' oder 'Scalpel' am Tisch gespielt haben, werden begeistert sein. Dieser revolutionäre Anti-Spin Belag ermöglicht es, sehr schnelle wie auch rotationsreiche Topspin-Bälle überaus gefährlich zu blocken.“
· „Der Gorilla ist ein recht schneller Antitop mit extrem glatter Oberfläche.“
· „Bewegt man den Schläger beim Schlag seitwärts, wird man mit krummen und nur schwer zu antizipierenden Flugkurven belohnt.“
· „Die Kontrolle ist jedoch nur mäßig. Das recht hohe Tempo verzeiht wenig Fehler.“
http://www.noppen-test.de/grizzly.php
„Ähnlich wie der "Affenbruder" Gorilla, hat der Grizzly eine sehr glatte Oberfläche, sie ist nur minimal griffiger. Das Tempo ist noch etwas höher, aufgrund des gefühlvollen Schwamms ist die Kontrolle jedoch nahezu identisch.“
Weitere Antitop-Schläger
http://www.noppen-test.de/new40.php
http://www.noppen-test.de/mirage.php
Das zu Grunde liegende Video ist nicht mehr verfügbar.
Das Spiel ist sehr gut zu verfolgen. Es sind keine Querbewegungen des Schlägers zu beobachten. Einige Bälle werden offensichtlich dadurch verschlagen, dass der Drall des ankommenden Balls durch das fortwährende Unter- oder mehr noch Überschneiden nicht richtig kompensiert wurde. Auch die Ballgeschwindigkeit hätte bei vielen Bällen höher sein können, da der Einsatz einer die Geschwindigkeit des Schlägers erhöhenden Körperdrehung nicht genutzt wurde. Die Topspin-Bälle kommen zwar hervorragend. Jedoch sollte die Richtung des Drallvektors aus taktischen Erwägungen immer wieder gewechselt werden. Der Magnuseffekt in horizontaler Richtung oder einer schiefliegenden Ebene wurde nicht genutzt. Das ist bedauerlich, denn wenn der Ball in der Horizontalen eine gekrümmte Bahn nimmt, kann man den Gegenspieler wesentlich mehr hin- und herlaufen lassen.
Der Topspin kann meist durch einen Spin, der eine schiefliegende Ebene der Flugbahn erzeugt, ersetzt werden. Der Weg der Querbewegung des Schlägers dürfte dabei etwas länger sein als der, der für die Erzeugung eines Topspins erforderlich ist, da die Hubarbeit für die Masse des Arms entfällt. Je nach Taktikerfordernis, kann man mit dem Magnuseffekt die Bahn nach links oder rechts lenken.
Bitte beurteilen Sie bei den folgenden Videos selbst, inwieweit die zuvor beschriebenen Ergebnisse angewendet worden sind.
https://www.youtube.com/watch?v=MI1N0anQJFY&feature=related
Tischtennis mit Timo Boll.
https://www.youtube.com/watch?v=DAVa1DD2c4E&feature=related
Timo Boll vs. Ma long 2008 World Cup Semifinal
https://www.youtube.com/watch?v=mdrNWgrfYiE&NR=1
ITTF World Cup 2009 - Timo Boll vs Ma Long Highlights
https://www.youtube.com/watch?v=qBtJXyK1Mvw&feature=related
Tischtennis mit Ma Lin und Wang Hao