Höhere Festigkeitslehre
Die Links wurden am 03.11.21 verifiziert und ergänzt.
Hier geht es im Wesentlichen um die Darstellung des Stoffverhaltens von Werkstoffen. Nicht behandelt werden die Themen, die bereits unter „Technische Mechanik“ zu finden sind.
· Beschreibung der Material- und Festigkeitseigenschaften von Werkstoffen, Gesamtdarstellungen
o Darstellung der Bewegung eines Punktes
o Lagrangesche und Eulersche Darstellung
o F, der Deformationsgradiententensor
o C, der rechte Cauchy-Green-Tensor
o E, der Greensche Verzerrungstensor
o Deformationsgeschwindigkeiten
o Infinitesimal kleine Verzerrungen
o Andere Stoffverhaltensmodelle
· Versagen von Werkstoffen durch Verformung oder Bruch
o Bruchkriterien und Bruchmechanik
o Anwendungen der Plastizitätstheorie
·
Text-Suche Kopiere eine Zeile aus einer Liste oder einen beliebigen
Text nach
Beschreibung der Material- und Festigkeitseigenschaften von Werkstoffen
https://lite.qwant.com/?q=Festigkeitslehre&p=2
Einführung in die Festigkeitslehre durch verschiedene Webseiten
http://www.uni-magdeburg.de/ifme/tm/pdf/Formelsammlung_Bertram.pdf
Enthält Formeln auch zur Festigkeitslehre
http://www.uni-magdeburg.de/ifme/zeitschrift_tm/1990_Heft2/Altenbach_H.pdf
Aspekte der klassischen Kontinuumsmechanik. Eine historische Übersicht
http://www.uni-magdeburg.de/ifme/l-festigkeit/pdf/Bertram-Gluege_Festkoerpermechanik2012.pdf
Buch, pdf: Festkörpermechanik, von Albrecht Bertram mit Beispielen von
Rainer Glüge
Beschreibung der Material- und Festigkeitseigenschaften von Werkstoffen
http://en.wikipedia.org/wiki/Continuum_mechanics
Die Kontinuumsmechanik ist ein Zweig der Mechanik, der sich mit dem
mechanischen Verhalten von Materialien befasst, die als kontinuierliche Masse
und nicht als diskrete Partikel modelliert werden.
Formulierung von Modellen, Kräfte in einem Kontinuum, Kinematik:
Bewegung und Verformung, Lagrange-Beschreibung, Eulersche Beschreibung,
Verschiebungsfeld Bilanzgesetze, Clausius-Duhem-Ungleichung
http://www.continuummechanics.org/index.html#TOC
Vektoren
Matrizen & Tensoren
Vektorrechnung
Tensornotation (Grundkenntnisse)
Tensornotation (Fortgeschritten)
Transformationen
Transformationsmatrizen
Divergenzsatz
Zylinderkoordinaten
EINFÜHRUNGSMECHANIK
Stress
Belastung
Hauptspannungen
Hookes Gesetz
Deformationen und Belastung
Verformungsgradienten
Polare Zersetzungen
Rotationsmatrizen
Green & Almansi
Invarianten
Hydrostatische und deviatorische
Dehnungen
Geschwindigkeitsverläufe
Wahre Belastung
STRESS
Hauptspannungen und Invarianten
Hydrostatische und deviatorische
Beanspruchungen
Von Mises Stress
Korotationale Derivate
Gleichgewicht
MATERIALVERHALTEN
Kontinuitätsgleichung
Navier Stokes-Gleichung
Thermodynamik
Hookes Gesetz
Plastizität von Metallen
Mooney-Rivlin Modelle
Dynamische Materialeigenschaften
Materialverhalten
http://en.wikipedia.org/wiki/Finite_strain_theory
In der Kontinuumsmechanik befasst sich die Theorie der endlichen Dehnung
- auch Theorie der großen Dehnung oder Theorie der großen Deformation genannt -
mit Deformationen, bei denen Dehnungen und / oder Rotationen groß genug sind,
um Annahmen zu entkräften, die der Theorie der infinitesimalen Dehnung inhärent
sind.
http://www-m6.ma.tum.de/~alt/alt-kontinuum.pdf
Mathematische Kontinuumsmechanik
Objektivität Kontinuumsmechanik, Objektivität für elastische Körper
S.145. Konstitutive Funktion für elastische Körper S.147
http://www.uni-magdeburg.de/ifme/l-festigkeit/pdf/Bertram-Gluege_Festkoerpermechanik2012.pdf
Buch, pdf: Festkörpermechanik, von Albrecht Bertram mit Beispielen von Rainer Glüge
https://www.researchgate.net/publication/324489094_Fundamentals_of_continuum_mechanics_-_classical_approaches_and_new_trends
Fundamentals of continuum mechanics – classical approaches and new trends
Die Grundgleichungen der Kontinuumsmechanik werden vorgestellt. Fortgeschrittene Modelle der Kontinuumsmechanik werden vorgestellt
http://www.civil.northwestern.edu/people/rudnicki/Continuum/cmbook_11_03_2011.pdf
Fundamentals of Continuum Mechanics
http://geo.mff.cuni.cz/vyuka/Martinec-ContinuumMechanics.pdf
CONTINUUM MECHANICS. GEOMETRY OF DEFORMATION, Measures of deformation, KINEMATICS, Material and spatial time derivatives, MEASURES OF STRESS, FUNDAMENTAL BALANCE LAWS, Energy equation, MOVING SPATIAL FRAME, Constitutive equation for isotropic materials, Application of the Clausius-Duhem inequality to a classical thermoelastic solid, Local balance laws in the spatial description, Isotropic linear elastic solid, Isotropic linear thermoelastic solid.
Konstitutive Gleichung für isotrope Materialien, Anwendung der Clausius-Duhem-Ungleichung auf einen klassischen thermoelastischen Festkörper, Lokale Gleichgewichtsgesetze in der räumlichen Beschreibung, Isotroper linearer elastischer Festkörper, Isotroper linearer thermoelastischer Festkörper
https://bilder.buecher.de/zusatz/20/20898/20898849_lese_1.pdf
Einige Grundlagen der Festkörpermechanik
http://www.mechbau.uni-stuttgart.de/ls2/Downloads/formelsammlung_CMKF.pdf
Formelsammlung
http://www.mm.bme.hu/~reith/Festigkeitslehre/Literatur/Heinze_TM2/TM-2.pdf
Skript
http://wandinger.userweb.mwn.de/HF/contents.html#Skripten
Skripte und Aufgaben
http://www.mb.uni-siegen.de/fkm/lehre/festigkeitslehre_ws12_13/kontaktmechanik_lv.pdf
Kontaktmechanik
https://en.wikipedia.org/wiki/Continuum_mechanics#Forces_in_a_continuum
Continuum mechanics
http://www.maschinenbau-wissen.de/skript3/mechanik/festigkeitslehre
Grundlagen der Festigkeitslehre
Statik und elementare Festigkeitslehre
Statik und Festigkeitslehre
http://wandinger.userweb.mwn.de/HF/index.html
Höhere Festigkeitslehre
Statik und Festigkeitslehre
Aufgabensammlung Technische Mechanik II
https://www.tuhh.de/mec/lehre/skripte-und-uebungen/technische-mechanik-i-iii-fuer-vt-lum.html
Zugang zu Vorlesungsskripten und Aufgaben. Umfangreich
https://www.tuhh.de/t3resources/mec/pdf/Scripte/Script_Elastostatik_SoSe14.pdf
Elastostatik
Festigkeitslehre
Statik und Festigkeitslehre
Statik und Festigkeitslehre. Übungsaufgaben
https://www.europa-lehrmittel.de/downloads-leseproben/54302-6/1705.pdf
Aufgaben zur Festigkeitslehre
https://lite.qwant.com/?q=aufgaben+zur+Festigkeitslehre
Aufgaben zur Festigkeitslehre
Aufgaben zur Festigkeitslehre
https://de.wikipedia.org/wiki/Formelsammlung_Tensoralgebra
Formelsammlung Tensoralgebra
https://de.wikipedia.org/wiki/Gau%C3%9Fscher_Integralsatz
Gaußscher Integralsatz
Variationsrechnung, Elastizität; auf Englisch
https://metager.de/meta/meta.ger3?eingabe=Tensoralgebra&submit-query=&focus=web&s=&f=&ff=&ft=&m=
Tensoralgebra
Im Folgenden soll ein Einblick in die Darstellung endlicher Deformationen gegeben werden. Hervorgehoben werden lokale Drehungen, weil sie für die Beschreibung des Materialversagens von großer Bedeutung sind.
https://biancahoegel.de/mechanik/verzerrungstensor.html
Verzerrungstensor.
Verschiedene Darstellungen
Darstellung der Bewegung eines Punktes
Zur Darstellung einer Bewegung werden Bezugssysteme verwendet. Am Beginn steht die Festlegung eines kartesischen Bezugsystems, auf das alle folgenden Systeme bezogen werden. In diesem Referenzsystem wird ein Punkt durch den Vektor Z und ein weiterer Punkt durch den Vektor z wie folgt dargestellt.
Z = X i + Y j + Z k z = x i + y j + z k
Als Deformation bezeichnet man, wenn ein Punkt Z in einen Punkt z überführt wird und die Punkte mit Massepunkten des Bereiches eines Körpers identifiziert werden.
Als Verschiebungsvektor u bezeichnet man einen Vektor mit den Komponenten
u = x – X v = y – Y w = z - Z
z = z(Z) und Z = Z(z) sind Funktionen, die diese Verschiebungen des Punktes Z in den Punkt z beschreiben sowie umgekehrt.
Z = Z(z) beschreibt die Referenz- oder. Ausgangskonfiguration eines Körpers. Die Konfiguration desselben Körpers unter Verwendung von Ortsvektoren z = z(Z) heißt die Momentankonfiguration des Körpers in Eulerschen Koordinaten z.
https://en.wikipedia.org/wiki/Finite_strain_theory
Finite strain theory
http://www.continuummechanics.org/deformationstrainintro.html
Deformations and Strain (Englisch)
http://www.mech.utah.edu/~brannon/public/Deformation.pdf
The mathematics of deformation. Auf Englisch. Viele Rechenbeispiele
Deformation and Strain. Simple Shear. Auf Englisch
Kinematik, S.17-32
http://www.files.ethz.ch/structuralgeology/jpb/files/struk/12verfor.pdf
Konzept der Verformung. Aus: Strukturgeologie 2016
https://lite.qwant.com/?q=Deformations+and+Strain+
Deformations and
Strain
https://metager.de/meta/meta.ger3?eingabe=Deformations+and+Strain+&submit-query=&focus=web
Deformations and Strain
Lagrangesche und Eulersche Darstellung
Bei der Eulerschen Betrachtungsweise bezieht sich der Beobachter auf einen festen Punkt im Raum. Er sieht den materiellen Punkt oder Bereich in die neue Position an sich vorbeiziehen. Der Beobachter kann keine Aussage über die Änderung der physikalischen Eigenschaften des Stoffes des Punktes oder Bereiches machen.
Bei der Lagrangeschen Formulierung
werden Änderungen verfolgt, die einem bestimmten Punkt der Masse zugeordnet
sind. Der Beobachter ist mit dem
materiellen Punkt verbunden. Er kann die Veränderung der physikalischen
Eigenschaften der Materie eines Punktes oder Bereiches verfolgen. Dafür benutzt er ein so genanntes konvektives
Koordinatensystem.
Die beiden verschiedenen Darstellungsarten spielen in der Dynamik der Flüssigkeiten und bei großen Deformationen eine Rolle.
https://de.wikipedia.org/wiki/Kontinuumsmechanik#Lagrange.E2.80.99sche_Betrachtungsweise
Lagrangesche Betrachtungsweise
https://de.wikipedia.org/wiki/Kontinuumsmechanik#Euler.E2.80.99sche_Betrachtungsweise
Eulersche Betrachtungsweise
https://en.wikipedia.org/wiki/Finite_strain_theory#Material_coordinates_.28Lagrangian_description.29
Lagrangesche Betrachtungsweise
https://en.wikipedia.org/wiki/Finite_strain_theory#Spatial_coordinates_.28Eulerian_description.29
Eulersche Betrachtungsweise
Relationship
between the material and spatial coordinate systems
Lagrangesche und Eulersche Darstellung
https://lite.qwant.com/?q=Lagrangesche+und+Eulersche+Darstellung
Lagrangesche und Eulersche Darstellung
F, der Deformationsgradiententensor
Der Deformationsgradient ist
F = grad x(X)
Mit ihm kann ein Geradenelement dX = X2 – X1 in ein Geradenelement dx = x2 – x1 transformiert werden.
F ist kein symmetrischer Tensor.
dx = F dX
Durch Transformation mit F wird aus dem Linienelement dX der Referenz- oder Ausgangskonfiguration ein Linienelement dx der Momentankonfiguration.
Dies entspricht geometrisch gesehen einer Drehung und einer Streckung eines beliebigen Geradenelementes (Achtung: nicht eines Punktes!) in einem Punkt des Raumes.
Die Determinante des Deformationsgradienten, det (F), wird als Jacobi-Determinante J bezeichnet. Mit der Definition eines Volumenelementes dV0 durch Basisvektoren in der Ausgangs- oder Referenzkonfiguration sowie des gleichen Volumenelementes, jedoch deformierten Volumenelementes in der Momentankonfiguration, erhält man die Euler-Gleichung
dV = J dV0.
https://de.wikipedia.org/wiki/Deformationsgradient
Deformationsgradient
https://en.wikipedia.org/wiki/Finite_strain_theory#Deformation_gradient_tensor
Deformation gradient tensor (Englisch)
https://de.wikipedia.org/wiki/Jacobimatrix
Jacobimatrix
https://lite.qwant.com/?q=Deformationsgradiententensor
Deformationsgradiententensor
Deformationsgradiententensor
https://metager.de/meta/meta.ger3?eingabe=Jacobimatrix&submit-query=&focus=web&s=&f=&ff=&ft=&m=
Jacobimatrix
https://lite.qwant.com/?q=Deformationsgradient
Deformationsgradient
https://www.biancahoegel.de/mechanik/kontinium/deformationsinvarianten.html
Deformationsinvarianten
https://www.biancahoegel.de/mathe/tensor/hauptinvariante.html
Hauptinvariante. Ableitungen der Hauptinvarianten
Spuren der Potenzen eines Tensors
Verwendung der Invarianten in Materialmodellen
Text-Suche Kopiere eine Zeile aus einer Liste oder einen beliebigen
Text nach
Die Deformation eines Körpers setzt sich aus einer Translation und einer Rotation des Starrkörpers sowie der Deformation des Körpers zusammen. Diese lässt sich wiederum in eine Drehung und eine Streckung zerlegen.
F = R U = V R
R ist der Dreh- oder Rotationstensor.
U ist der rechte Strecktensor und V der linke Strecktensor.
https://de.wikipedia.org/wiki/Polarzerlegung
Polarzerlegung
https://lite.qwant.com/?q=polare+Zerlegung+eines+Tensors
polare Zerlegung eines Tensors
https://de.wikipedia.org/wiki/Deformationsgradient#Polare_Zerlegung
Polare Zerlegung
http://www.math.uni-bonn.de/people/woermann/Polarzerlegung.pdf
Polarzerlegung
https://de.wikipedia.org/wiki/Kontinuumsmechanik#Verzerrungstensoren
Verzerrungstensoren
https://www.uni-due.de/imperia/md/content/mathematik/ag_neff/diplomarbeit_kuhlmann_29.10.10.pdf
Verzerrungsenergie eines elastisch deformierten Körpers. Einfache Scherung S.17-20
Suchen bei http://scholar.google.de/ nach: Kontinuumsmechanik: Ein Grundkurs für Ingenieure und Physiker Von Ralf Greve
Links-Streck-Tensor V
Suchen bei http://scholar.google.de/ nach: Kontinuumsmechanik: Ein Grundkurs für Ingenieure und Physiker Von Ralf Greve; Drehtensor
Auf S.19, 1.2.4, wird gesagt, R repräsentiere eine
Starrkörperrotation. Diese Aussage ist auch bei anderen Autoren zu finden. Sie
trifft aber nicht zu. Siehe dazu das „fundamental theorem“, welches auf
Arbeiten von Cauchy zurückgeht: Fundamental Theorem: “The deformation of any point may be regarded as resulting from a translation,
a rigid rotation of the prinicipal axes of strain
and stretches along these axes.“
https://metager.de/meta/meta.ger3?eingabe=Drehtensor&submit-query=&focus=web&s=&f=&ff=&ft=&m=
Drehtensor
Demnach ist
dx = F dX = R U dX
Aus dieser Gleichung kann man ersehen, dass die Deformation eines Geradenelementes bei X im allgemeinen Fall aus einer Streckung dieses Geradenelementes und einer Drehung besteht. Wir betrachten im Folgenden die Drehung am Beispiel der einfachen Scherung, die als die Deformation eines Rhombus gleicher Höhe definiert ist.
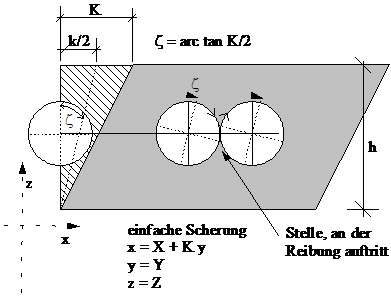
Es handelt sich bei der Drehung nicht um eine Starrköperdrehung eines Bereiches eines Körpers oder des ganzen Körpers, sondern nur um die Drehung eines einzigen Linienelementes mit zwei Punkten, die Anfang und Ende markieren. Liegen zwei Linienelemente dicht beieinander und haben sie eine (nicht notwendigerweise unterschiedliche) Drehung zwischen der Referenz- und der Momentankonfiguration gemacht, so entsteht zwischen ihnen an den Endpunkten eine Kraft, die die Drehung verhindern will. Wird die Festigkeit zwischen den Endpunkten zweier Elemente überschritten, so tritt Zerstörung ein. Aus diesem Grund ist die Darstellung des Stoffverhaltens ausschließlich durch Streckungen für viele Stoffarten unzureichend. Sehr eindrücklich kann man diesen Unterschied wahrnehmen, wenn man über einen Kiesweg und einen Splittweg läuft. Die Erklärung des wesentlichen Unterschieds in deren Festigkeitsverhalten kann nur durch die Berücksichtigung von R erfolgen. Hieran schließt sich die Frage an, ob es nicht genügen würde, für die Darstellung des Stoffverhaltens ein Maß von R zu verwenden. Ausführlich wird hierüber berichtet in „Prinzipien der klassischen Mechanik und Feldtheorie, Band III/1; Springer-Verlag, 1960, Editor: S. Flügge“, S.274, c Rotation.
Experimentell wurde die „einfache Scherung“ zum ersten Mal im Jahre 1976 erzeugt. Drei der damals ermittelten Diagramme sind nachfolgend dargestellt.
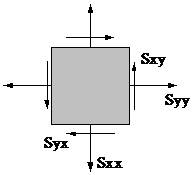
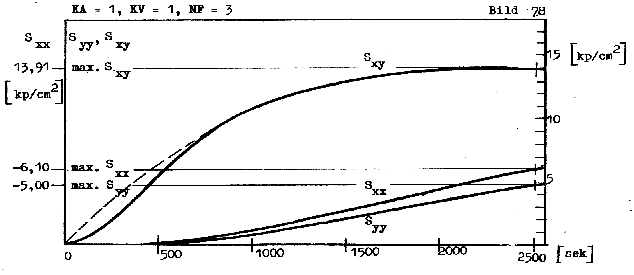
Bild: Spannungen am Einheitskörper infolge einfacher Scherung. 1 kp=9,8066 N
Schergeschwindigkeit dμ/dt=10^-4 * 0,333 1/s. Stoff: Gussasphalt.
Die Strich-Strich-Linie stellt die Approximation durch eine Stoffverhaltensgleichung vom Differenzialtyp dar.
Sie wird hier nicht wiedergegeben.
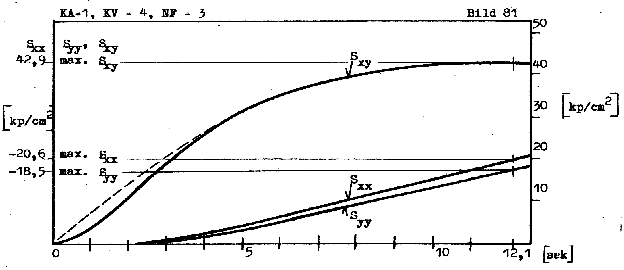
Bild: Spannungen am Einheitskörper infolge einfacher Scherung. 1 kp=9,8066 N
Schergeschwindigkeit dμ/dt=10^-4 * 41,666 1/s. Stoff: Gussasphalt
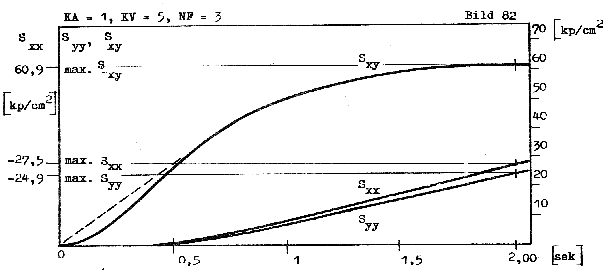
Bild: Spannungen am Einheitskörper infolge einfacher Scherung. 1 kp=9,8066 N
Schergeschwindigkeit dμ/dt=10^-4 * 208,3 1/s. Stoff: Gussasphalt
Die Diagramme zeigen eine starke Abhängigkeit der Spannungen von der Verformungsgeschwindigkeit.
Die einfache Scherung ist eine das Volumen erhaltende, so genannte isochore Deformation. Es gibt daneben auch eine Streckung, bei der ebenfalls das Volumen erhalten wird. Bei ihr ist R = E, dem Einheitstensor.
https://en.wikipedia.org/wiki/Deformation_(mechanics)#Simple_shear
Deformation-Mechanics
https://metager.de/meta/meta.ger3?eingabe=einfache+Scherung+&submit-query=&focus=web&s=&f=&ff=&ft=&m=
einfache Scherung
https://metager.de/meta/meta.ger3?eingabe=simple+shear&submit-query=&focus=web&s=&f=&ff=&ft=&m=
simple shear
Suchen bei http://scholar.google.de/ nach: Kontinuumsmechanik: Ein Grundkurs für Ingenieure und Physiker Von Ralf Greve; einfache Scherung
Text-Suche Kopiere eine Zeile aus einer Liste oder einen beliebigen
Text nach
C, der rechte Cauchy-Green-Tensor
Der rechte Cauchy-Green-Tensor C ist definiert als
C = FT F = U2
Durch diese Multiplikation wird erreicht, dass C ein symmetrischer Tensor ist. Er ist der Ausgangspunkt für den Greenschen Verzerrungstensor, der üblicherweise für die Darstellung elastischen Stoffverhaltens eingesetzt wird. C lässt sich auf eine Diagonalform transformieren.
Man kann aus der Gleichung erkennen, dass mit ihm ein Informationsverlust über die Deformation eines Körpers verbunden ist, nämlich der über die lokale Drehdeformation. Dies mag zu brauchbaren Ergebnissen führen, solange nicht die innere Struktur eines Stoffes durch die Deformation leidet oder zerstört wird.
http://de.wikischolar.org/wiki/Kartenprojektionen:_Cauchy-Green_Tensor
Der Cauchy-Green-Tensor
https://www.biancahoegel.de/mechanik/strecktensor.html
Strecktensor
Der rechte Cauchy-Green-Tensor
Ein Beispiel
https://www.biancahoegel.de/mechanik/strecktensor.html
Hauptinvarianten des rechten Cauchy-Green-Tensors
Suchen
bei http://scholar.google.de/ nach: Berechnung
C in:
Kontinuumsmechanik: Ein Grundkurs für Ingenieure und Physiker Von Ralf Greve; Rechts-Cauchy-Green-Tensor C
https://www.biancahoegel.de/mathe/tensor/hauptinvariante.html
E, Greenscher Verzerrungstensor
Mit Hilfe des Metriktensors G der Ausgangskonfiguration kann der Greensche Verzerrungstensor definiert werden.
E = (C – G)/ 2
E ist invariant gegenüber Starrköperbewegungen.
E ist ein symmetrischer Tensor.
G ist in der Regel der Einheitstensor mit Werten 1 auf der Diagonalen.
Greenscher Verzerrungstensor
https://lite.qwant.com/?q=Greenscher+Verzerrungstensor
Greenscher Verzerrungstensor
Suchen bei http://scholar.google.de/ nach: Berechnung E (hat dort das Symbol G) in: Kontinuumsmechanik: Ein Grundkurs für Ingenieure und Physiker Von Ralf Greve; Greenscher-Verzerrungstensor
Suchen bei http://scholar.google.de/ nach: Berechnung der Größen bei kleiner Deformation in: Kontinuumsmechanik: Ein Grundkurs für Ingenieure und Physiker Von Ralf Greve; Momentan- und Referenzkonfiguration
D Verzerrungsgeschwindigkeitstensor
https://de.wikipedia.org/wiki/Kontinuumsmechanik#Verzerrungsgeschwindigkeiten
Verzerrungsgeschwindigkeiten
Numerische und experimentelle Untersuchungen zu Transportvorgängen in Schneckenmaschinen
Anwendung der konstitutiven Gleichungen in einem Beispiel. Verzerrungsgeschwindigkeitstensor
http://newmaeweb.ucsd.edu/~vlubarda/research/pdfpapers/amr-04.pdf
Thermoelasticity, Elastoplasticity, Rate of deformation
https://biancahoegel.de/mechanik/verzerrungstensor.html
Verzerrungstensor.
Verschiedene Darstellungen
Suchen bei http://scholar.google.de/ nach: Numerische Beanspruchungsanalyse von Rissen: Finite Elemente in der ... Von Meinhard Kuna Deformationsgeschwindigkeiten
Infinitesimal kleine Verzerrungen
https://en.wikipedia.org/wiki/Infinitesimal_strain_theory
Ausführliche Darstellung (in englischer Sprache)
https://en.wikipedia.org/wiki/Strain_tensor#Infinitesimal_strain_tensor
Infinitesimal strain tensor
Infinitesimal strain tensor
https://de.wikipedia.org/wiki/Kontinuumsmechanik#Geometrische_Linearisierung
Geometrische Linearisierung
https://lite.qwant.com/?q=Infinitesimal+kleine+Verzerrungen
Infinitesimal kleine Verzerrungen
https://en.wikipedia.org/wiki/Stress_measures
Stress measures
https://en.wikipedia.org/wiki/Stress_(physics)
Stress
https://de.wikipedia.org/wiki/Kontinuumsmechanik#Spannungstensoren
Spannungstensoren
https://www.biancahoegel.de/mechanik/spannungstensor.html
Spannungstensor
https://de.wikipedia.org/wiki/Cauchysches_Fundamentaltheorem
Cauchysches Fundamentaltheorem
https://de.wikipedia.org/wiki/Cauchysches_Fundamentaltheorem#Der_Cauchy.E2.80.99sche_Spannungstensor
Der Cauchysche Spannungstensor
https://en.wikipedia.org/wiki/Cauchy_stress_tensor
Cauchy stress tensor
https://de.wikipedia.org/wiki/Hauptspannung#Hauptspannung_und_Hauptspannungsrichtung
Hauptspannung und Hauptspannungsrichtung
http://www.uni-magdeburg.de/ifme/l-festigkeit/pdf/fl-5.pdf
Zerlegung des Spannungstensors S.114
https://en.wikipedia.org/wiki/Cauchy_stress_tensor#Principal_stresses_and_stress_invariants
Principal stresses and stress invariants
https://de.wikipedia.org/wiki/Eigenwert
Eigenwerte einer Matrix
https://de.wikipedia.org/wiki/Hauptspannung#Hauptspannung_und_Hauptspannungsrichtung
Hauptspannung und Hauptspannungsrichtung
https://en.wikipedia.org/wiki/Stress_(mechanics)#Alternative_measures_of_stress
Piola-Kirchhoff-Spannungen
Suchen bei http://scholar.google.de/ nach: Kontinuums- Und Kontaktmechanik: Synthetische Und Analytische Darstellung Von Kai Willner Cauchy-Spannungen
Suchen bei http://scholar.google.de/ nach: Kontinuums- Und Kontaktmechanik: Synthetische Und Analytische Darstellung Von Kai Willner Piola-Kirchhoff-Spannungen
Text-Suche Kopiere eine Zeile aus einer Liste oder einen beliebigen
Text nach
https://en.wikipedia.org/wiki/Solid_mechanics
Solid mechanics
https://en.wikipedia.org/wiki/Frame_of_reference
Bezugssystem
http://www-m6.ma.tum.de/~alt/alt-kontinuum.pdf
Mathematische Kontinuumsmechanik
Objektivität Kontinuumsmechanik, Objektivität für elastische Körper S.145. Konstitutive Funktion für elastische Körper S.147
http://www.qucosa.de/recherche/frontdoor/?tx_slubopus4frontend[id]=265
Kontinuumsmechanische Grundlagen des Stoffverhaltens, dargestellt an einem Stoff
Prizip der materiellen Objektivität
Suchen bei http://scholar.google.de/ nach: Kontinuums- Und Kontaktmechanik: Synthetische Und Analytische Darstellung Von Kai Willner Materielle Objektivität
Suchen bei http://scholar.google.de/ nach: Kontinuumsmechanik: Ein Grundkurs für Ingenieure und Physiker Von Ralf Greve
Prinzip der materiellen Objektivität
Suchen bei http://scholar.google.de/ nach: Kontinuumsmechanik: Elastisches und inelastisches Verhalten isotroper und ... Von Josef Betten. Stoffgleichungen
https://en.wikipedia.org/wiki/3-D_elasticity
Linear elasticity
Elastizitätstheorie
Materialtheorie, S.54-64
https://en.wikipedia.org/wiki/3-D_elasticity#See_also
Weiterführende Links
https://en.wikipedia.org/wiki/Hooke%27s_law
Hooke´s law
https://en.wikipedia.org/wiki/Poisson%27s_ratio
Poisson ratio
http://www-m6.ma.tum.de/~alt/alt-kontinuum.pdf
Nichtlineare Elastizität S.231
http://tuprints.ulb.tu-darmstadt.de/935/1/Doktorarbeit.pdf
Symmetrien, Erhaltungssätze und Bilanzgleichungen in verallgemeinerten Elastizitätstheorien mit Mikrostruktur und
Eichfeldtheorien der Versetzungen
Bei http://scholar.google.de/ suchen nach: Finite Elemente in der Statik und Dynamik Von Michael Link, Das Hookesche Gesetz
Suchen bei http://scholar.google.de/, Mechanik der festen Körper By Heinz Parkus, Grundlagen der Elastizitätstheorie
http://www.mech-wilmanski.de/cottbusthermomech.pdf
Lineare Thermoelastizität
https://lite.qwant.com/?q=Thermoelastizit%C3%A4t
Thermoelastizität
Bilanzgleichungen, Thermomechanik, S.40-53
Bei http://scholar.google.de/ suchen nach: Finite Elemente in der Statik und Dynamik Von Michael Link, , Wärmedehnungsvektor
https://de.wikipedia.org/wiki/Viskoelastizit%C3%A4t
Viskoelastizität
http://www-brs.ub.ruhr-uni-bochum.de/netahtml/HSS/Diss/BockholdJoerg/diss.pdf
Nichtlineare Modellierung des Kriechens und der Relaxation von Beton. Modelle zur Beschreibung zeitlich verzögerter Verformungen
https://en.wikipedia.org/wiki/Creep_(deformation)
Creep
http://www.ifm.kit.edu/download/Doll_Stefan.pdf
Zur numerischen Behandlung großer elasto-viskoplastischer Deformationen bei isochor-volumetrisch entkoppeltem Stoffverhalten
http://matperso.mines-paristech.fr/Donnees/data04/422-emsat.pdf
Mechanics of Cosserat media
https://metager.de/meta/meta.ger3?eingabe=Cosserat+media+&submit-query=&focus=web&s=&f=&ff=&ft=&m=
Mechanics of Cosserat
media
https://en.wikipedia.org/wiki/Continuum_mechanics#Forces_in_a_continuum
Forces in continuum
Suchen bei http://scholar.google.de/ nach: Kontinuumsmechanik: Elastisches und inelastisches Verhalten isotroper und ... Von Josef Betten. Viskoelastische Stoffe
Versagen von Werkstoffen durch Verformung oder Bruch
Bruchkriterien und Bruchmechanik
https://de.wikipedia.org/wiki/Bruchmechanik
Bruchmechanik
https://en.wikipedia.org/wiki/Tensile_strength
Tensile strength
https://de.wikipedia.org/wiki/Bruchkriterium
Bruchkriterium
https://de.wikipedia.org/wiki/Linear-elastische_Bruchmechanik
Linearelastische Bruchmechanik
https://de.wikipedia.org/wiki/Linear-elastische_Bruchmechanik#Spannungsintensit.C3.A4tsfaktoren
Spannungsintensitätsfaktoren
http://www.peterknoedel.de/lehre/bruchmech/bruchmech_04-05-10.pdf
Bruchmechanik
Suchen bei http://scholar.google.de/ nach: Numerische Beanspruchungsanalyse von Rissen: Finite Elemente in der ... Von Meinhard Kuna Grundlagen der Bruchmechanik
Suchen bei http://scholar.google.de/ nach: Numerische Beanspruchungsanalyse von Rissen: Finite Elemente in der ... Von Meinhard Kuna FEM-Techniken zur Rissanalyse
Suchen bei http://scholar.google.de/ nach: Umformtechnik multimedial: Werkstoffverhalten, Werkstückversagen, Werkzeuge ... Von Josef Reissner; Werkzeugversagen
https://en.wikipedia.org/wiki/Plasticity_(physics)
Plasticity
https://en.wikipedia.org/wiki/Plastic_deformation_in_solids
Plastic deformation in solids
https://en.wikipedia.org/wiki/Yield_stress
Yield
https://en.wikipedia.org/wiki/Yield_strength
Yield strength
Plastizität S.202
http://tuprints.ulb.tu-darmstadt.de/epda/000312/Grammenoudis_MikropolarePlastizitaet.pdf
Mikropolare Plastizität
Plastizität. Materialverhalten
Suchen bei http://scholar.google.de/ nach: Ingenieurmechanik: Deformierbare Körper, Band 2 Von Mahir B. Sayir,Jürg Dual,Stephan Kaufmann Plastizität
Suchen bei http://scholar.google.de/ nach: Kontinuumsmechanik: Elastisches und inelastisches Verhalten isotroper und ... Von Josef Betten. Plastisches Verhalten isotroper und anisotroper Stoffe
Anwendungen der Plastizitätstheorie
Plastische Traglast
https://lite.qwant.com/?q=Plastische+Traglast
Plastische Traglast
https://lite.qwant.com/?q=Flie%C3%9Fgelenktheorie
Fließgelenktheorie
Fließgelenktheorie
Text-Suche Kopiere eine Zeile aus einer Liste oder einen beliebigen
Text nach
https://de.wikipedia.org/wiki/Isotropie#Transversale_Isotropie_in_der_Werkstoffkunde
Isotropie
https://en.wikipedia.org/wiki/Poisson%27s_ratio#Isotropic_materials
Isotrope Stoffe
https://en.wikipedia.org/wiki/3-D_elasticity#Anisotropic_homogeneous_media
Anisotrope homogene Stoffe
Anisotrope homogene Stoffe
Anisotropie
http://tuprints.ulb.tu-darmstadt.de/epda/000964/dissertation_broese_part_1.pdf
Grundlagen zur Beschreibung von Anisotropie, S.15. Rotationseffekte in
der Kristallplastizität. Grundlagen der Kontinuumsmechanik S.9, Transformation
des Modells auf die Momentankonfiguration S.39, Numerische Rechnungen mit den
Polykristall-Modellen S.143
Aufgaben aus der
Kontinuumsmechanik
http://www.continuummechanics.org/index.html#TOC
13 Aufgaben aus der Kontinuumsmechanik
http://wandinger.userweb.mwn.de/HF/contents.html#Skripten
Skripte und Aufgaben