Kinematik einer Bewegung mit nicht konstanter Beschleunigung

Für die allgemeine Bewegung gilt

a = dv/ dt

v = ∫a dt + v₁

v = ds/ dt ds= v ^. dt s = ∫v dt + s₁

s = ∫(∫a dt + v₁) dt + s₁

Es werden die Dimensionen s, m vereinbart.

Intervall (0,1)

Der Weg beginnt bei 0.

Die Geschwindigkeit am Punkt 0 sei 10.

Die Beschleunigung am Punkt 0 sei 1 und nehme nach folgender Funktion

bis zum Punkt 1 linear auf den Wert 0 ab.

Der Punkt 2 sei nach 7 Sekunden erreicht.

Zu ermitteln sind der Weg und die Geschwindigkeit im Punkt 1.

An den Stellen, an denen zunächst Punkte eingetragen sind, sollen die fehlenden Werte errechnet werden.

a(0) = 1 a(1) = 0 m/s²

v(0) = 10 v(1) = … 13,5 m/s

s(0) = 0 s(1) = … 87,9 m

t(0) = 0 t(1) = 7 s

Aus dieser Gleichung wird durch Integration die Geschwindigkeit im Punkt 1 berechnet. Sie wird gewählt, weil die Randwerte von a im Intervall (0,1) bekannt sind.

Annahme (Aufgabenstellung):

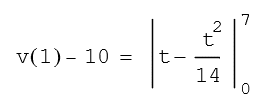
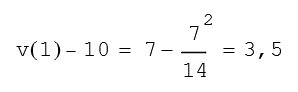
Die Funktion der Geschwindigkeit wird dadurch ermittelt, dass statt des bestimmten Integrals das unbestimmte Integral gelöst wird.

Aus folgender Gleichung wird durch Integration der Weg im Punkt 1 berechnet. Sie wird gewählt, weil nunmehr die Randwerte von v im Intervall (0,1) bekannt sind.

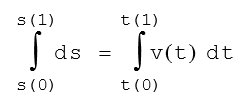
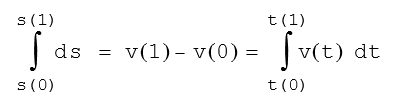
Intervall (1,2)

Die Länge des Weges im Intervall Δs(1,2) = 10,10 ist gegeben.

Die Geschwindigkeit soll in diesem Intervall konstant sein (gleichförmige Bewegung).

Wegen der Vorgabe einer gleichförmigen Bewegung ist die Beschleunigung a in diesem Intervall konstant=0.

Zu ermitteln ist die Zeit, die im Punkt 2 vergangen ist.

a(1) = 0 a(2) = 0 m/s²

v(1) = 13,5 v(2) = 13,5 m/s

s(1) = 87,9 s(2) = 87,90 + 10,10 = 98 m

t(1) = 7 t(2) = … 7,75 s

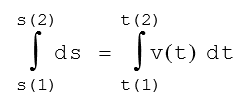
S(2) – s(1) = v(1)^.(t(2) – t(1))

10,1 = 13,5^.(t(2) – 7)

t(2) = 10,1/ 13,5 + 7 = 7,75

Intervall (2,3)

In diesem Intervall erfolgt eine Bremsung (Verzögerung) bis zum Stillstand. Der Wert der Verzögerung ist gegeben.

Zu ermitteln ist der Gesamtweg und die Gesamtzeit.

a(2) = -6,5 a(3) = -6,5 m/s²

v(2) = 13,5 v(3) = 0 m/s

s(2) = 98 s(3) = … 112,04 m

t(2) = 7,75 t(3) = … 9,83 s

Aus dieser Gleichung wird durch Integration die Zeit im Punkt 3 berechnet, da die Randwerte v bekannt sind.

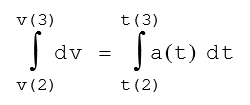
Da a keine Funktion von t ist, sondern eine Konstante, ist die Integration besonders einfach.

v(3) – v(2) = a(2)^.(t(3) – t(2))

0 – 13,5 = -6,5(t(3) – 7,75)

Da die obere Grenze der Zeit nicht bekannt ist, wird eine Variable für die Zeit eingeführt.

v(t) := v(3) = 0 (Stillstand)

t := t(3)

v(t) -13,5 = - 6,5(t – 7,75)

v(t) = 13,5 – 6,5(t – 7,75)

-13,5 = -6,5^.t(3) + 6,5^.7,75

6,5^.t(3) = 13,5 + 6,5^.7,75

t(3) = 9,83

Aus dieser Gleichung wird durch Integration der gesamte im Punkt 3 zurückgelegte Weg berechnet.

Die Funktion der Geschwindigkeit von der Zeit hatten wir zuvor berechnet. Um die Klarheit des Berechnungsganges zu bewahren, nehmen wir keine Vereinfachungen vor.
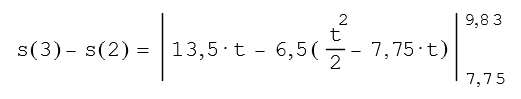