Kreisprozess im p-V-Diagramm berechnen

Ein ideales Gas mit dem Volumen V₁, dem Druck p₁ und der Temperatur T₁ wird adiabatisch auf ein Volumen V₂ komprimiert. Dann wird es isobar auf die Temperatur T₃ erwärmt und danach isotherm auf das Volumen V₄ expandiert. Durch eine isochore Abkühlung wird es in den Ausgangszustand gebracht.

Stellen Sie den Kreisprozess in einem p-V-Diagramm maßstabsgerecht dar.

Die gegebenen Werte sind in der folgenden Tabelle zu finden. Die Werte für die freien Felder sind zu berechnen.

Punkt	V [Liter]	p [kPa]	T [K]
1	3,1	2,1	320
2	1,0
3			490
4

Der Adiabatenexponent ist κ=1,3

Lösung

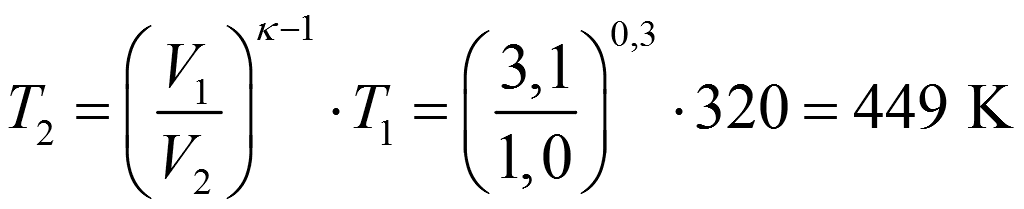
Punkt	V [Liter]	p [kPa]	T [K]
1	3,1	2,1	320
2	1,0	9,14	449
3	1,091	9,14	490
4	3,1	3,22	490